Az 1849-es 2 forintos kincstári utalvány sorozatjelölésének és sorszámozásának rendszere.

A 1848–49-es forradalom papírpénzeit gyűjtők körében biztosan feltűnt, hogy a Kossuth-bankók a modern bankjegyekhez mérten összetett sorozatjelöléssel rendelkeznek (nagy és kis betűk kombinációja, esetleg további sorszám, nyomtatva és kézzel is írva). Ez idáig nem sokan foglalkoztak azzal, hogy rendszerbe szedjék a forradalom papírpénzeinek sorozatváltozatait. A legkisebb mennyiségben a 100 forintosok után az 1849-es 2 forintosok voltak nyomtatva. A kis nyomtatott mennyiségnek köszönhetően kevés a sorozatváltozat, a nagy gyakoriságuk miatt ezek könnyen összegyűjthetőek. Az összegyűjtött több mint 150 darab 2 forintos sorozatának és sorszámának kielemzése meglepő eredményt hozott.
 GT – nagy sorozat g. – kicsi sorozat 40599 – sorszám
GT – nagy sorozat g. – kicsi sorozat 40599 – sorszám
A sorozat esetében a következő nagy betűjelekkel ismertek példányok:
EE, EZ, GE, GZ, GT, GQ, GJ, GW, GR, GD
Az EZ és GD sorozattal ellátott papírpénzek mind ívből vágott sorszám nélküliek voltak.
EE, EZ, GE, GZ, GT, GQ nagy sorozat esetében a kicsi betűjel a következők közül került ki:
| z. | t. | q. | a. | s. | h. | b. | n. | g. | e. |
GJ, GW, GR, GD esetében pedig:
| w. | ? | u. | d. | x. | l. | ű. | f. | o. | i. |
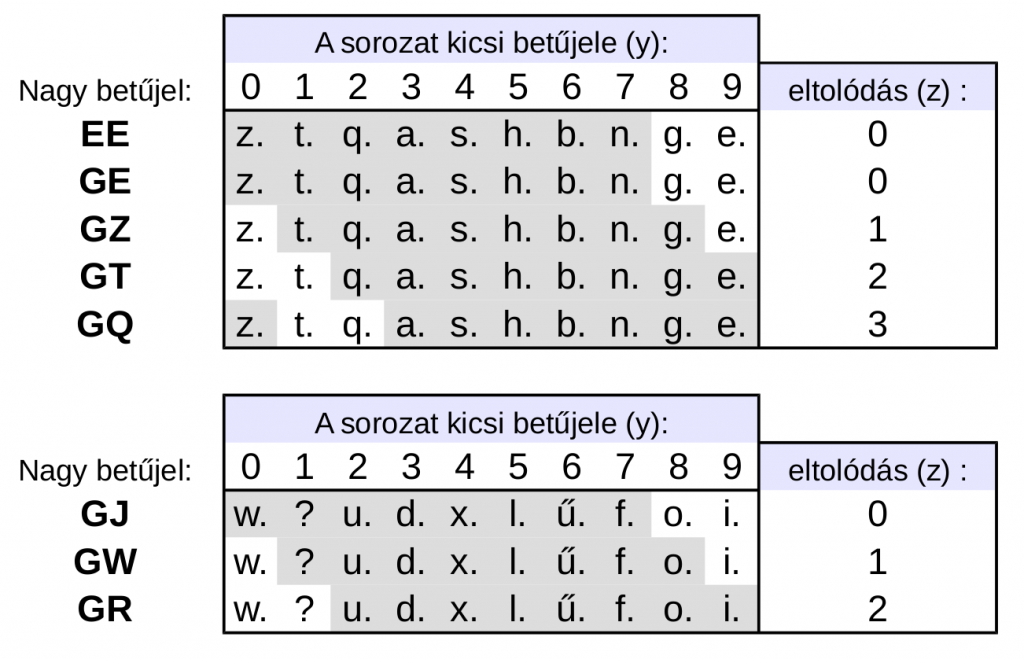
Minden egyes nagy sorozathoz nyolc egymást követő kis betűjel tartozik a tízből. Táblázatba foglalva:
Szürkével van jelölve, hogy a 10 kis betűjelből melyik az a 8, amelyik az adott nagy sorozatjelöléshez tartozik. Például GT sorozatnál ezek a q. a. s. h. b. n. g. e. kis betűjelek. Minden egyes nagy sorozatjelöléshez tartozik egy “eltolódás” érték. GT sorozatnál ez az érték 2, ugyanis első kis betűjelnek, a q.-nek a számszerű értéke 2 (a táblázat tetején 0-tól 9-ig).
A sorozat és a sorszám között a következő matematikai összefüggés van:
((x – 1) mod 8) + z = y
x – sorszám
z – az adott nagy sorozathoz tartozó “eltolódás” értéke
y – sorozat kicsi betűjelének számszerű értéke.
Mod, vagyis modulo, osztás utáni maradék kiszámolásának művelete. (pl. 19 mod 8 = 3)
Példákkal bemutatva:
GT q. / 14057
14057 – 1 = 14056
14056 osztva 8 … maradék: 0
GT-hez tartozó eltolódás: 2
0 + 2 = 2
A sorozat kis betűjelének értéke 2, vagyis q.
GJ ű. / 66943
66943 – 1 = 66942
66942 osztva 8 … maradék: 6
GJ-hez tartozó eltolódás: 0
6 + 0 = 6
A sorozat kis betűjelének értéke 6, vagyis ű.
Felmerül a kérdés, vajon mi célt szolgálhatott egy ilyen összetett számozási rendszer használata? Vélhetően hamisítás elleni védelem része volt. Ha hamisították volna, a hamisítók az ismeretek hiányában nem tudták volna megfelelően sorszámozni a pénzeket, így a fent elvégzett számítás segítségével azonnal kiderült volna, hogy a sorszámozás és a sorozat megjelölése matematikailag nem illeszkedik egymáshoz (a számítás eredményeként más kicsi betűjel jön ki), vagyis a pénzjegy hamisítvány.
Szintén, ha valaki utólag tölti ki a sorszámot egy számozatlan példányon, nagy valószínűséggel megállapítható, hogy a számozás nem korabeli.
– KP